30-second summary
Coulomb’s Law
Coulomb’s law is a law of physics that describes the electric forces that act between electrically charged particles.
The magnitude of the electric force F is directly proportional to the amount of one electric charge, q1, multiplied by the other, q2, and inversely proportional to the square of the distance between the particles.
Coulomb’s law has many applications to modern life, from Xerox machines, laser printers, electrostatic air cleansing to powder coating.

About Coulomb’s Law
Coulomb’s law is a law of physics that describes the electric forces that act between electrically charged particles. This law should be remembered because it is one of the vital concepts in electricity. Coulomb’s law operates in the world of atoms and nuclei (e.g., electrons in an atomic cloud), as well as in everyday life (e.g., static electricity).
The equation for the electrostatic forces acting on the particles is called Coulomb’s law after Charles-Augustin de Coulomb, whose experiments in 1785 led him to it. Coulomb found that the electric force, like the magnetic force, varied inversely as the square of the distance. In fact, the equation he used to express variation of electrical force with distance was quite analogous to the one he found for magnetic forces.
Coulomb’s Law has a many applications to modern life, from Xerox machines, laser printers, electrostatic air cleansing to powder coating.
Coulomb’s Law Equation
Coulomb’s law can be used to calculate the force between charged particles (e.g., two protons) or between two charged objects. The magnitude of the electric force F is directly proportional to the amount of one electric charge, q1, multiplied by the other, q2, and inversely proportional to the square of the distance between the particles. Coulomb’s Law is stated as the following equation.

This is the scalar form of the Coulomb’s law, which gives the magnitude of the vector of the electrostatic force F between two point charges, but not its direction. Here, K or ke is Coulomb’s constant (ke ≈ 8.988×109 N⋅m2⋅C−2), q1 and q2 are the signed magnitudes of the charges, and the scalar r is the distance between the charges. The greater the charge on the objects, the greater the electrostatic field. The greater the distance between the objects, the weaker the electrostatic field between them, and vice versa. If q1 and q2 are both either positively or negatively charged, the force is repulsive. If q1 and q2 are opposite polarity or charge, the force is attractive. The proportionality of the electric force to 1/r2 has been verified with great precision.
Thus, 1C is that amount of charge which, if placed on each of two point objects that are 1.0 m apart, will result in each object exerting a force of:
(9.0×109 N-m2/C2)x(1.0C)x(1.0C)/(1.0m)2 = 9.0 x 109N
This is an enormous force. We rarely encounter charges as large as a coulomb. Charges produced by rubbing ordinary objects (such as a comb or plastic ruler) are typically around a microcoulomb (?C = 10-6 C) or less.
The same charges are repelled and the opposite charges are attracted. The base unit of electric charge is the (negative) charge of the electron, 1.602×10-19 coulombs. The electric force is operative between charges down to distances of at least 10-16 metre, or approximately one-tenth of the diameter of atomic nuclei.
Coulomb’s Law in Vector Form
Coulomb’s law may be expressed also by its vector form. Let’s also focus on particle 1 and write the force acting on it in terms of a unit vector that points along a radial axis extending through the two particles, radially away from particle 2. As with other unit vectors, has a magnitude of exactly 1 and no unit. With these decisions, we write the electrostatic force as:

where r is the distance between the particles and k is a positive constant called the Coulomb constant.
Coulomb Constant
The value of the proportionality constant in Coulomb’s law depends on the system of units used. In our study of electricity and magnetism we will use SI units exclusively. The SI electric units include most of the familiar units such as the volt, the ampere, the ohm, and the watt. (There is no British system of electric units.) The SI unit of electric charge is called one coulomb (1C).
The Coulomb constant is used in many electric equations, although it is sometimes expressed as the following product of the vacuum permittivity constant:

From now on, we will usually write Coulomb’s law as:

Problem with Solution: Coulomb’s Law
Two point charges (q1 = 20nC and q2 = -70nC) are separated by a distance r = 1cm. Find the magnitude and direction of the electric force that q1 exerts on q2 and that q2 exerts on q1.

Use Coulomb’s law to solve this problem that asks for the electric forces that two charges exert on each other. The signs of the charges will determine the directions of the forces.
Solution:
After converting the units of distance to meters and the units of electric charge to coulombs, Coulomb’s Law gives us:
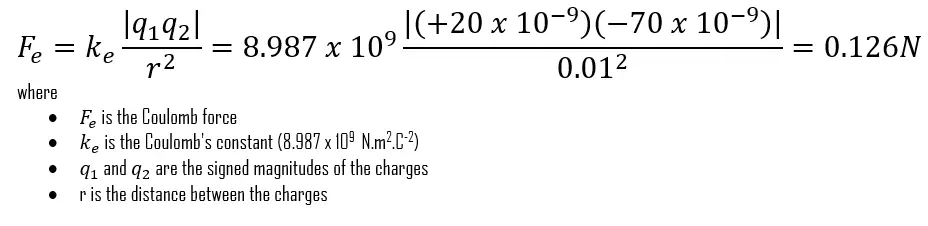
The charges have opposite signs, so the force is attractive; that is, the force that acts on q2 is directed toward q1 along the line joining the two charges.
Another Example: Electric Charge
Noteworthy, in four liters of water, there is about 2.1 x 108C of total electron charge. Thus, if we place two bottles a meter apart, the electrons in one of the bottles repel those in the other bottle with a force of 4.1 x 1026N. This tremendous force is comparable with the force that the planet Earth would weigh if weighed on another Earth. Ut, as was written, there are also positive (protons) and these charges tend to cancel each other out.
Coulomb Force in Atomic Nuclei
Coulomb forces act a very important role determining stability of atomic nuclei. Atomic nuclei consist of protons and neutrons, which attract each other through the nuclear force, while protons repel each other via the electric force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons, which form stable nuclei.
Neutrons stabilize the nucleus because they attract each other and protons, which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many or too few neutrons for a given number of protons, the resulting nucleus is not stable and undergoes radioactive decay.
Frequently asked questions
Coulomb’s Law has a many applications to modern life, from Xerox machines, laser printers, electrostatic air cleansing to powder coating.
Coulomb’s law can be used to calculate the force between charged particles (e.g., two protons) or between two charged objects. The magnitude of the electric force F is directly proportional to the amount of one electric charge, q1, multiplied by the other, q2, and inversely proportional to the square of the distance between the particles.
The electrons in an atom are attracted to the protons in the nucleus by the electromagnetic force. This force binds the electrons inside an electrostatic potential well surrounding the smaller nucleus, which means that an external source of energy is needed for the electron to escape.
The coulomb (symbol: C) is the International System of Units (SI) unit of electric charge. The coulomb was defined as the quantity of electricity transported in one second by a current of one ampere: 1 C = 1 A × 1 s


