30-second summary
Gauss’s law
“Gauss’s law states that the net electric flux through any hypothetical closed surface is equal to 1/ε0 times the net electric charge within that closed surface. “
Surface S1: The electric field is outward for all points on this surface. Thus, the flux of the electric field through this surface is positive, and so is the net charge within the surface, as Gauss’ law requires.
Surface S2: This surface encloses no net charge because the enclosed positive and negative charges have equal magnitudes. Gauss’ law requires that the net flux of the electric field through this surface be zero.
Surface S3: This surface encloses no charge, and thus qenclosed =0. Gauss’ law requires that the net flux of the electric field through this surface be zero. That is reasonable because all the field lines pass entirely through the surface, entering it on the right and leaving on the left.
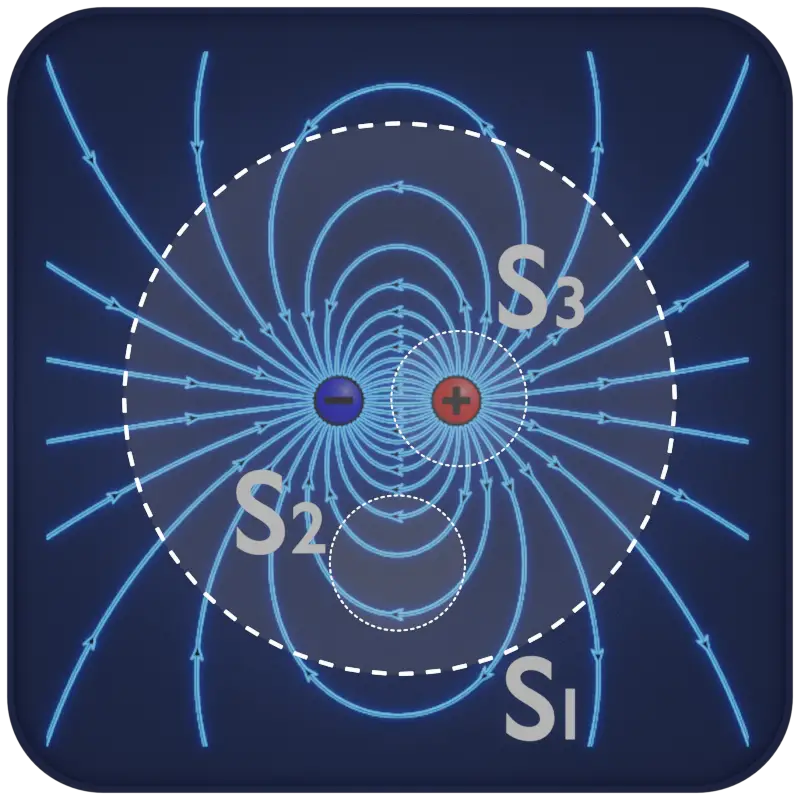
Two particles, with charges equal in magnitude but opposite in sign, and the field lines describing the electric fields the particles set up in the surrounding space. Three Gaussian surfaces are also shown, in cross-section.
About Gauss’s law
In electromagnetism, Gauss’s law, also known as Gauss’s flux theorem, relates the distribution of electric charge to the resulting electric field. In its integral form, Gauss’s law relates the charge enclosed by a closed surface (often called as Gaussian surface) to the total flux through that surface. When the electric field, because of its symmetry, is constant everywhere on that surface and perpendicular to it, the exact electric field can be found. Gauss’ law and Coulomb’s law are different ways of describing the relation between charge and electric field in static situations. In such special cases, Gauss’s law is easier to apply than Coulomb’s law. Gauss’s law involves the concept of electric flux, a measure of how much the electric field vectors penetrate through a given surface.
Gauss’s law is useful method for determining electric fields when the charge distribution is highly symmetric. It was developed by Mr. Carl Friedrich Gauss, a German mathematician and physicist.
Like Ampere’s law, which is analogous to magnetism, Gauss’ law is one of four Maxwell’s equations (the first) and thus fundamental to classical electrodynamics.
What is Electric Flux
Gauss’s law involves the concept of electric flux, which refers to the electric field passing through a given area. In words:
Gauss’s law states that the net electric flux through any hypothetical closed surface is equal to 1/ε0 times the net electric charge within that closed surface.
ΦE = Q/ε0
In pictorial form, this electric field is shown as a dot, the charge, radiating “lines of flux”. These are called Gauss lines. Note that field lines are a graphic illustration of field strength and direction and have no physical meaning. The density of these lines corresponds to the electric field strength, which could also be called the electric flux density: the number of “lines” per unit area. Electric flux is proportional to the total number of electric field lines going through a surface.
Electric flux depends on the strength of electric field, E, on the surface area, and on the relative orientation of the field and surface. For a uniform electric field E passing through an area A, the electric flux E is defined as:
Φ = E x A
This is for the area perpendicular to vector E. We generalize our definition of electric flux for a uniform electric field to:
Φ = E x A x cosφ (electric flux for uniform E, flat surface)
What happens if the electric field isn’t uniform but varies from point to point over the area ? Or what if is part of a curved surface? For a non-uniform electric field, the electric flux dΦE through a small surface area dA is given by:
dΦE = E x dA
We calculate the electric flux through each element and integrate the results to obtain the total flux. The electric flux ΦE is then defined as a surface integral of the electric field:

Gauss’s law formula – Integral
In its integral form, Gauss’s law relates the charge enclosed by a closed surface to the total flux through that surface. The precise relation between the electric flux through a closed surface and the net charge Qencl enclosed within that surface is given by Gauss’s law:
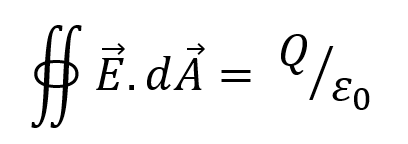
where ε0 is the same constant (permittivity of free space) that appears in Coulomb’s law. The integral on the left is over the value of E on any closed surface, and we choose that surface for our convenience in any given situation. The charge Qencl is the net charge enclosed by that surface.
It doesn’t matter where or how the charge is distributed within the surface. Any charge outside this surface must not be included. A charge outside the chosen surface may affect the position of the electric field lines, but will not affect the net number of lines entering or leaving the surface.
Gauss’s law formula – Differential
Gauss’s law can be used in its differential form, which states that the divergence of the electric field is proportional to the local density of charge. This divergence theorem is also known as Gauss’s-Ostrogradsky’s theorem.
Application of Gauss’s Law
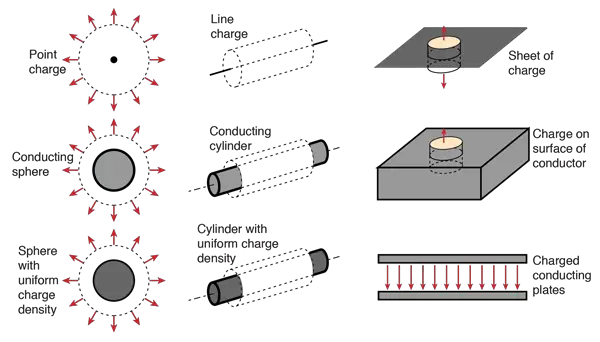
Gauss’s law is useful for determining electric fields when the charge distribution is highly symmetric. In choosing the surface, always take advantage of the symmetry of the charge distribution so that E can be removed from the integral.
In order to apply Gauss’s law, however, we must choose the “gaussian” surface very carefully so we can determine E. We normally try to think of a surface that has just the symmetry needed so that E will be constant on all or on parts of its surface.
Frequently asked questions
Gauss’s law is useful for determining electric fields when the charge distribution is highly symmetric. In choosing the surface, always take advantage of the symmetry of the charge distribution so that E can be removed from the integral.
Like Ampere’s law, which is analogous to magnetism, Gauss’ law is one of four Maxwell’s equations (the first) and thus fundamental to classical electrodynamics.
The coulomb (symbol: C) is the International System of Units (SI) unit of electric charge. The coulomb was defined as the quantity of electricity transported in one second by a current of one ampere: 1 C = 1 A × 1 s

