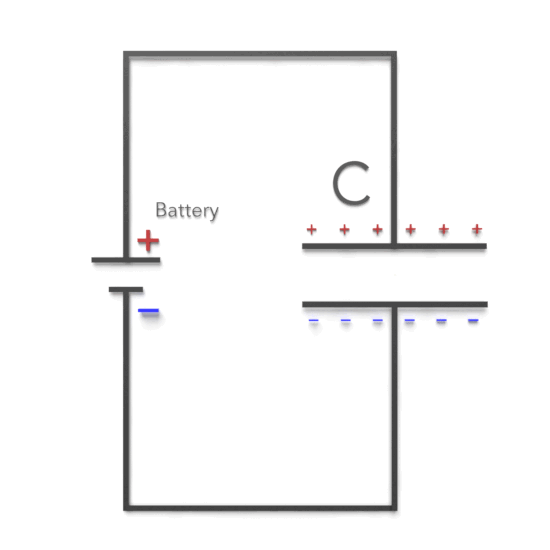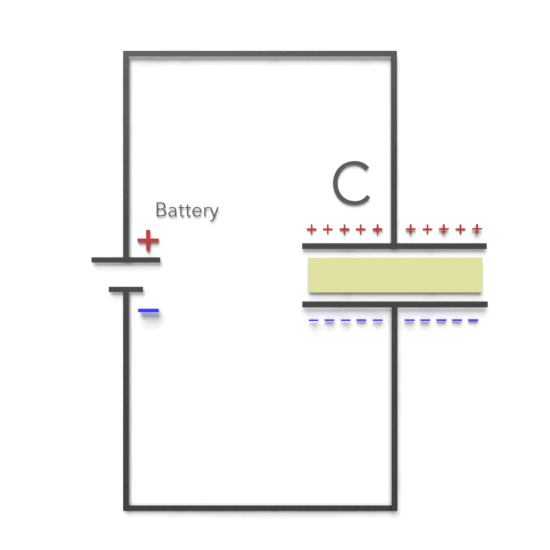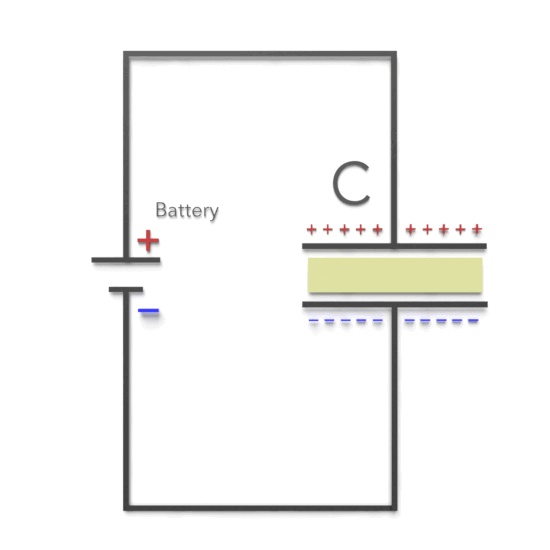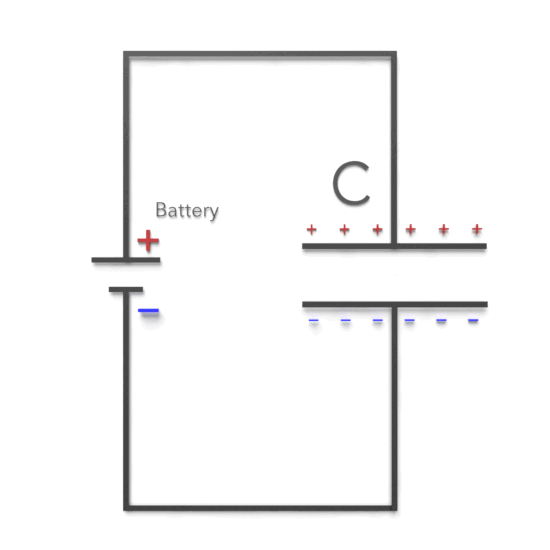
RC circuits, consisting of resistors (R) and capacitors (C), are fundamental building blocks in electrical and electronic systems. These circuits exhibit unique behavior during charging and discharging processes, making them suitable for various applications, including filters, timers, and integrators.
Charging Process:
When an RC circuit is connected to a DC voltage source, the capacitor begins to charge. During the charging process, the voltage across the capacitor increases, while the current through the resistor decreases. The key equations for the charging process are:
- Voltage across the capacitor: Vc(t) = V_source * (1 – e^(-t/τ))
- Current through the resistor: I(t) = (V_source / R) * e^(-t/τ)
- Time constant (τ) for the RC circuit: τ = R * C
Discharging Process:
When the voltage source is disconnected, and the capacitor is allowed to discharge through the resistor, the voltage across the capacitor and the current through the resistor decrease over time. The key equations for the discharging process are:
- Voltage across the capacitor: Vc(t) = V_initial * e^(-t/τ)
- Current through the resistor: I(t) = (V_initial / R) * e^(-t/τ)
- Time constant (τ) for the RC circuit: τ = R * C
Applications:
- Filters: RC circuits can be used as low-pass or high-pass filters, attenuating specific frequencies while allowing others to pass through. In a low-pass filter configuration, the output is taken across the capacitor, while in a high-pass filter configuration, the output is taken across the resistor.
- Timers: RC circuits can be utilized as timers or pulse generators, creating time delays or producing time-dependent waveforms. By selecting appropriate resistor and capacitor values, the desired time delay or waveform characteristics can be achieved.
- Integrators and Differentiators: RC circuits can also function as integrators or differentiators, performing mathematical operations on input signals. In an integrator configuration, the output is taken across the capacitor, and in a differentiator configuration, the output is taken across the resistor.
- Smoothing Circuits: RC circuits can be employed as smoothing circuits in power supply applications, reducing voltage fluctuations and ripple in the output.
Understanding the behavior, equations, and applications of RC circuits is crucial for designing and analyzing various electrical and electronic systems. These fundamental circuits are widely used in signal processing, timing, control, and power supply applications, making them an essential topic for engineers and technicians.
Example of Calculation
An RC (Resistor-Capacitor) circuit is a simple electrical circuit composed of a resistor and a capacitor connected either in series or parallel. Here, we will discuss a series RC circuit, which is a common configuration. The voltage across the capacitor and the current through the circuit change over time when the circuit is charged or discharged.
Let’s consider an example of an RC circuit calculation involving a charging capacitor:
Given values:
- Voltage source (V_source): 10 V
- Resistor (R): 1 kΩ (1000 Ω)
- Capacitor (C): 10 µF (10 × 10^(-6) F)
We will calculate the voltage across the capacitor (V_C) and the current through the circuit (I) at a specific time (t) after the circuit starts charging.
- Calculate the time constant (τ) of the RC circuit: τ = R × C τ = 1000 Ω × 10 × 10^(-6) F = 0.01 s
The time constant (τ) indicates the time required for the voltage across the capacitor to reach approximately 63.2% of its final value (V_source) or the time needed for the current to decrease to 36.8% of its initial value.
- Choose a specific time (t) after the circuit starts charging: For this example, let’s pick t = 0.005 s (half of the time constant).
- Calculate the voltage across the capacitor (V_C) at time t: V_C(t) = V_source × (1 – e^(-t/τ)) V_C(0.005) = 10 V × (1 – e^(-0.005/0.01)) V_C(0.005) ≈ 10 V × (1 – e^(-0.5)) ≈ 10 V × (1 – 0.6065) ≈ 3.935 V
At t = 0.005 s, the voltage across the capacitor is approximately 3.935 V.
- Calculate the current through the circuit (I) at time t: I(t) = (V_source – V_C(t)) / R I(0.005) = (10 V – 3.935 V) / 1000 Ω ≈ 6.065 mA
At t = 0.005 s, the current through the circuit is approximately 6.065 mA.
This example demonstrates how to calculate the voltage across the capacitor and the current through the circuit at a specific time after the RC circuit starts charging. The same approach can be used for a discharging capacitor, with some modifications to the equations.