The potential energy of a dipole in an electric field is given by U = -P * E * cos(θ), where P is the dipole moment, E is the field strength, and θ is the angle between them.
Potential Energy of a Dipole in an Electric Field
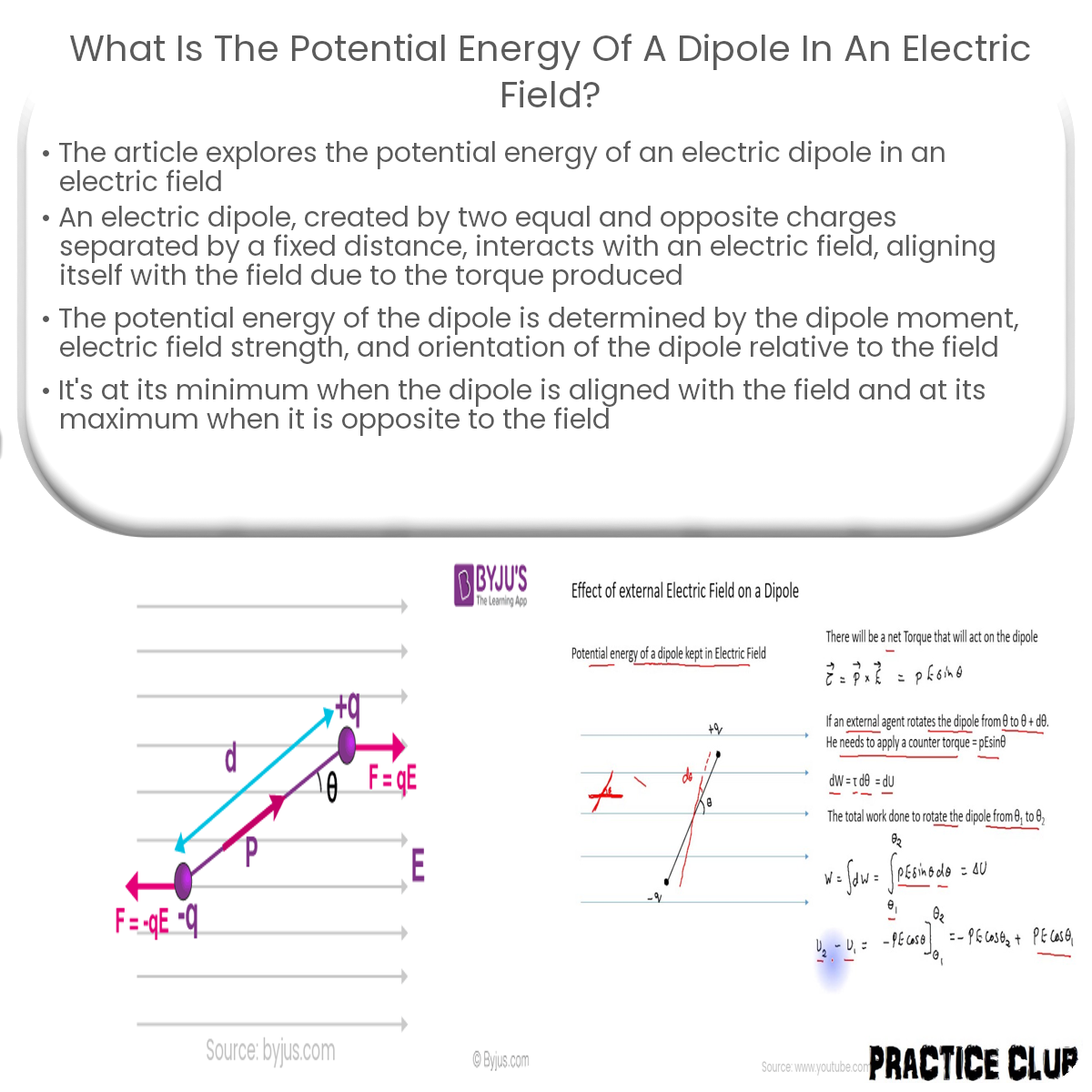
Electric dipoles are created when two equal and opposite charges are separated by a fixed distance. They play a significant role in the study of electromagnetism, as they help to describe the interactions of molecules and other systems in electric fields. This article will discuss the potential energy of a dipole in an electric field and the factors that influence it.
Understanding Electric Dipoles
An electric dipole is represented by a vector called the dipole moment, denoted by P. The dipole moment is the product of the charge magnitude q and the distance d between the charges:
P = q * d
Interaction of Dipoles with Electric Fields
When an electric dipole is placed in an electric field, the field exerts a force on each charge, creating a torque that tries to align the dipole with the field. The torque τ can be calculated using the following equation:
τ = P * E * sin(θ)
Where E is the electric field strength, and θ is the angle between the dipole moment vector and the electric field vector.
Potential Energy of a Dipole in an Electric Field
The potential energy U of a dipole in an electric field is the work done to rotate the dipole from its initial orientation to a specific angle in the field. The potential energy can be determined by integrating the torque with respect to the angle:
U = -P * E * cos(θ)
This formula indicates that the potential energy is at its minimum when the dipole moment vector is aligned with the electric field (θ = 0), and it is at its maximum when the dipole moment vector is opposite to the electric field (θ = 180°).
Factors Influencing Potential Energy
- Dipole moment: A larger dipole moment will result in a higher potential energy, as the charges and the distance between them are greater.
- Electric field strength: The strength of the electric field has a direct impact on the potential energy of the dipole. A stronger field leads to a higher potential energy.
- Orientation: The angle between the dipole moment vector and the electric field vector affects the potential energy. The closer the alignment, the lower the potential energy.
In conclusion, the potential energy of a dipole in an electric field depends on the dipole moment, the electric field strength, and the orientation of the dipole with respect to the field. Understanding these factors is essential for predicting the behavior of dipoles in various electric field scenarios.