30-second summary
Thermoelectricity
Thermoelectricity is generated by the thermoelectric effect, which is the direct conversion of temperature differences to electric voltage and vice versa via a thermocouple. Heating two joined dissimilar materials will cause a transfer of electrons between the materials setting up a current flow.
In different materials, the Seebeck coefficient is not constant in temperature, and so a spatial gradient in temperature can result in a gradient in the Seebeck coefficient. If a current is driven through this gradient, then a continuous version of the Peltier effect will occur. The Thomson effect describes the resulting electric current that develops in a single conductor when a small temperature gradient is applied.
See more: Thermoelectric effect
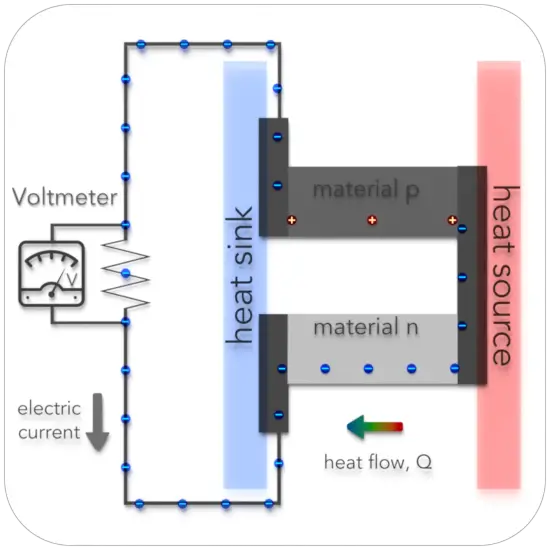
Thermoelectricity
Thermoelectricity is generated by the thermoelectric effect, which is the direct conversion of temperature differences to electric voltage and vice versa via a thermocouple. Heating two joined dissimilar materials will cause a transfer of electrons between the materials setting up a current flow.
The term “thermoelectric effect” encompasses three separately identified effects:
- Seebeck effect. The Seebeck effect is a phenomenon in which a temperature difference between two dissimilar electrical conductors or semiconductors produces a voltage difference between the two substances. If a temperature gradient exists at a junction of two dissimilar conductors connected electrically in series and thermally in parallel, a voltage is produced. This potential drop is the result of the thermoelectric effect first reported by Thomas Seebeck in 1821. Seebeck focused primarily on the power generating properties of a thermocouple known as the Seebeck effect. The voltage generated depends on the Seebeck coefficient S (S = V/ΔT) and the temperature difference between the two junctions in the thermocouple.
- Peltier effect. The Peltier effect is the analog to the Seebeck effect. The Peltier effect is the presence of heating or cooling at an electrified junction of two different conductors and is named after French physicist Jean Charles Athanase Peltier, who discovered it in 1834. Instead of generating a potential difference across C and D with junctions J1 and J2 held at different temperatures, the Peltier effect uses an electromotive source to drive a current, heating one junction and cooling the other. The effect can be quantitatively described by the Peltier coefficient. The Peltier coefficient (π) is determined by the ratio of the current, (I) to the rate of heating (q): π = I/q. It represents how much heat is carried per unit charge. The sign of π is determined by which junction is heated and which is cooled. A typical Peltier heat pump involves multiple junctions in series, through which a current is driven. Some of the junctions lose heat due to the Peltier effect, while others gain heat. Thermoelectric heat pumps exploit this phenomenon, as do thermoelectric cooling devices found in refrigerators.
- Thomson effect. In different materials, the Seebeck coefficient is not constant in temperature, and so a spatial gradient in temperature can result in a gradient in the Seebeck coefficient. If a current is driven through this gradient, then a continuous version of the Peltier effect will occur. The Thomson effect describes the resulting electric current that develops in a single conductor when a small temperature gradient is applied. This relationship is described by the equation; q = βIΔT, where q is the rate of heating, I is an electric current, ΔT is the change in temperature, and β is the Thomson coefficient. Lord Kelvin, tied all three of the thermoelectric coefficients together in the Kelvin relationships. These equations describe how the Seebeck, Peltier, and Thomson coefficients interrelate.
The Peltier effect can be considered as the back-action counterpart to the Seebeck effect: if a simple thermoelectric circuit is closed, then the Seebeck effect will drive a current, which in turn (by the Peltier effect) will always transfer heat from the hot to the cold junction. The close relationship between Peltier and Seebeck effects can be seen in the direct connection between their coefficients:
The second Thomson relation:
Π = TS
where Π is the Peltier coefficient, T is the absolute temperature, and S is the Seebeck coefficient.

