Reed-Solomon decoders detect and correct errors in digital communication systems, ensuring data integrity in storage, broadcast, and more.

Understanding the Reed-Solomon Decoder

The Reed-Solomon (RS) decoder is an integral component of error correction techniques used in various digital communication systems. Invented by Irving S. Reed and Gustave Solomon in 1960, the Reed-Solomon codes have become crucial in applications ranging from satellite and deep-space communication to data storage, QR codes, and more. In this article, we delve into the essential aspects of a Reed-Solomon decoder and its significance in modern digital communication.

Reed-Solomon Codes: An Overview

Reed-Solomon codes are a class of non-binary error-correcting codes known for their ability to correct multiple errors in a data block. They belong to the broader category of block codes, which means that they work on fixed-size blocks of data. RS codes have a unique feature that sets them apart from other error-correcting codes: they can correct both random and burst errors. Random errors are isolated bit flips in a data stream, while burst errors are clusters of adjacent bit errors that occur simultaneously.

The RS codes’ error-correcting capability is determined by a parameter called ‘minimum distance,’ which represents the minimum number of symbol changes needed to convert one valid code to another. The higher the minimum distance, the more errors the code can correct.

Role of the Reed-Solomon Decoder

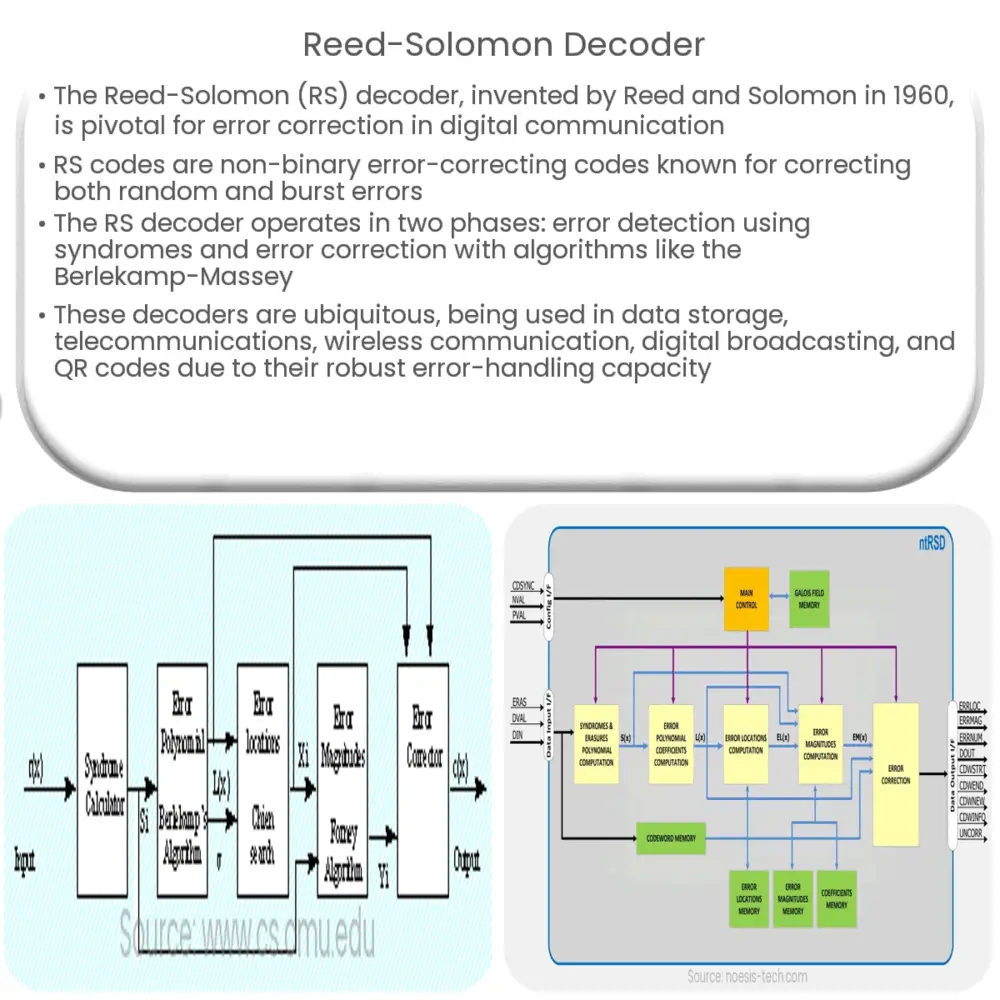
The primary function of a Reed-Solomon decoder is to detect and correct errors that may have occurred during the transmission or storage of data. The decoding process can be divided into two main steps: error detection and error correction.

Error Detection: In this step, the RS decoder calculates the syndromes for the received data block. Syndromes are the remainders obtained when the received data is divided by the generator polynomial, which is a mathematical representation of the RS code. If the syndromes are all zero, it indicates that no errors are present in the data. However, if there are non-zero syndromes, the decoder proceeds to the error correction step.

Error Correction: To correct the errors, the RS decoder uses a variety of algorithms. One common method is the Berlekamp-Massey algorithm, which computes the error locator polynomial – a polynomial whose roots indicate the locations of errors in the data block. Once the error locations are identified, the decoder can then calculate and correct the error values, thus recovering the original data.

Applications of Reed-Solomon Decoders

Reed-Solomon decoders have found widespread use in diverse fields due to their robust error-correction capabilities. Some of the most common applications include:

• Data Storage: RS decoders are used in CDs, DVDs, and Blu-ray discs to recover data despite physical imperfections or scratches on the disc surface.
• Telecommunications: Satellite and deep-space communication systems rely on RS decoders to maintain the integrity of transmitted data over long distances and in the presence of noise.
• Wireless Communication: Mobile phone networks and Wi-Fi systems also employ RS decoders to ensure reliable data transmission in the face of interference and fading.

Digital Broadcasting

Digital Television: Reed-Solomon decoders are employed in digital television systems like DVB-T, ATSC, and ISDB-T to maintain the quality and reliability of transmitted video and audio data. RS codes help mitigate the effects of noise, interference, and multipath propagation on the received signal, providing viewers with a clear, high-quality viewing experience.

Digital Radio: Similarly, digital radio systems like DAB and DRM use Reed-Solomon codes to ensure reliable and clear reception of audio broadcasts. The RS decoders help recover the original audio signal despite interference and fading caused by the radio environment.

QR Codes and Barcodes

Reed-Solomon codes are also employed in QR codes and certain types of barcodes, such as PDF417 and MaxiCode. RS decoders ensure that the encoded data remains readable and intact, even if the code is partially damaged or obscured. This robustness makes Reed-Solomon codes an ideal choice for these applications, where physical wear and tear or poor printing quality could compromise the readability of the codes.

Conclusion

Reed-Solomon decoders have played a vital role in maintaining the integrity and reliability of digital communication systems across various fields. Their ability to correct multiple random and burst errors makes them indispensable in the face of noise, interference, and other factors that could compromise data transmission. As digital communication continues to evolve, Reed-Solomon decoders will undoubtedly remain a crucial tool for ensuring the quality and dependability of our information systems.

Further Reading

For those interested in learning more about Reed-Solomon codes and their applications, consider the following resources:

1. Wicker, S. B., & Bhargava, V. K. (1994). Reed-Solomon codes and their applications. New York: IEEE Press.
2. Lin, S., & Costello Jr., D. J. (2004). Error Control Coding: Fundamentals and Applications (2nd ed.). Upper Saddle River, NJ: Prentice-Hall.
3. MacWilliams, F. J., & Sloane, N. J. A. (1977). The Theory of Error-Correcting Codes. Amsterdam: North-Holland.

These resources provide a comprehensive overview of the theory and implementation of Reed-Solomon codes, as well as their practical applications in various fields.