To calculate the magnetic field of a permanent magnet, use Gilbert’s model, Ampere’s law, Biot-Savart law, or numerical methods like finite element method.
Calculating Magnetic Field Produced by a Permanent Magnet
The magnetic field generated by a permanent magnet depends on its size, shape, and the material from which it is made. The field can be calculated using a few basic equations and principles from magnetostatics. This article will discuss some methods for calculating the magnetic field produced by a permanent magnet.
Gilbert’s Model
One of the earliest and simplest models for calculating magnetic fields is Gilbert’s model, which assumes that the magnet can be represented by a set of magnetic dipoles or magnetic charges. The magnetic field strength (H) at any point in space can be calculated using the formula:
H = μ0 * (magnetization / 4π * distance)
Here, μ0 is the permeability of free space, magnetization is the magnetization vector of the magnet, and the distance is the distance between the point of interest and the magnetic dipole.
Ampere’s Law
Ampere’s law can also be used to calculate the magnetic field produced by a permanent magnet. Ampere’s law states that the line integral of the magnetic field around any closed loop is equal to the total current enclosed by that loop. This can be expressed as:
∮B • dl = μ0 * Ienc
Using this law, we can determine the magnetic field at a point in space due to the magnet. However, applying Ampere’s law directly can be complicated for non-symmetric magnets or those with complex shapes.
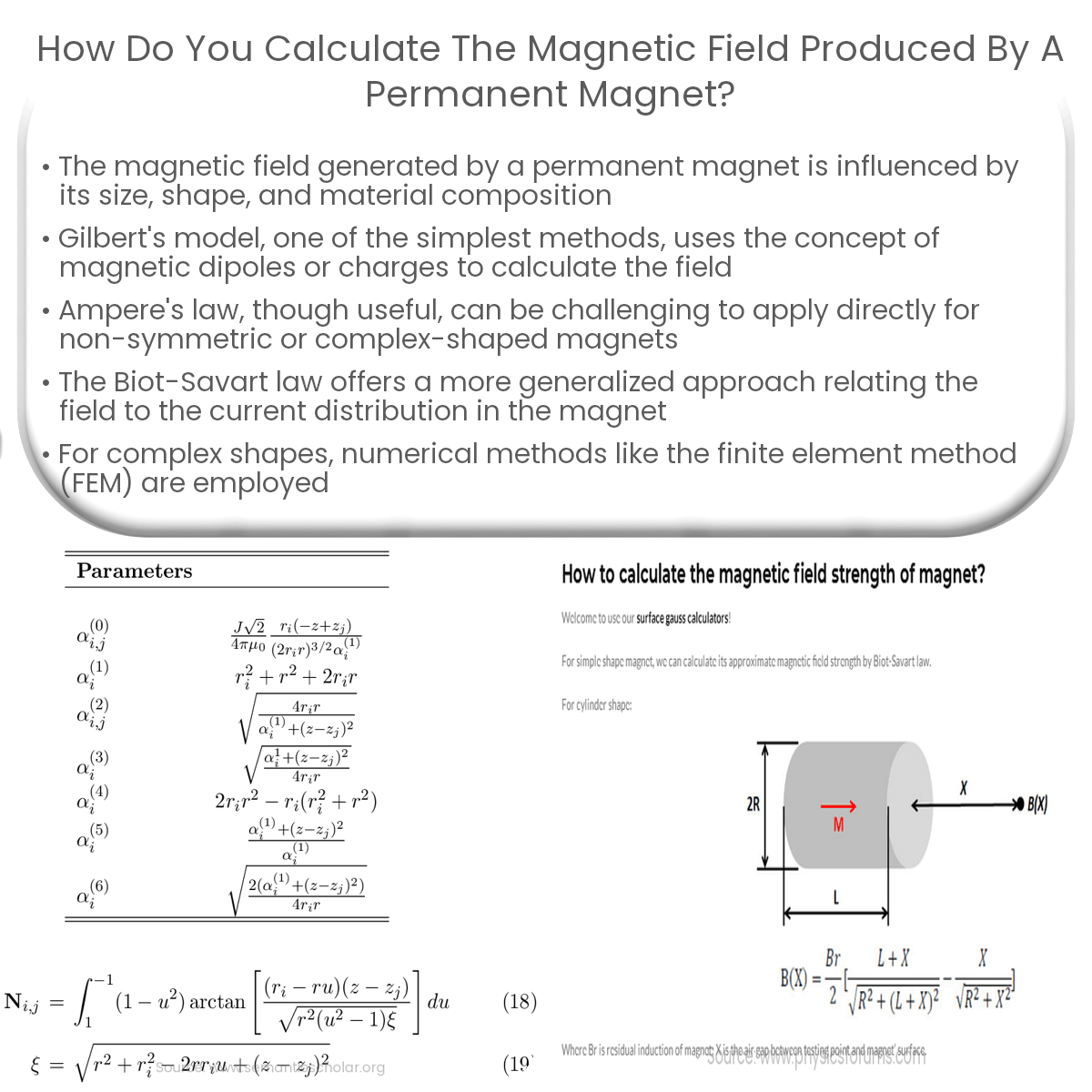
Biot-Savart Law
The Biot-Savart law provides a more general approach to calculating the magnetic field produced by a permanent magnet. It relates the magnetic field at a point in space to the current distribution in the magnet. The Biot-Savart law can be written as:
B = (μ0 / 4π) * ∫(I * dl × r̂) / r2
Here, I is the current, dl is the differential length element, r̂ is the unit vector pointing from the source to the point of interest, and r is the distance between them. This law can be used for any magnet shape, but the integration process can be complex.
Numerical Methods
For complex magnet shapes and configurations, numerical methods like the finite element method (FEM) can be used to calculate the magnetic field. These methods divide the problem into smaller, more manageable parts and solve them using computer algorithms.
In conclusion, calculating the magnetic field produced by a permanent magnet involves applying principles from magnetostatics, such as Gilbert’s model, Ampere’s law, or the Biot-Savart law. Numerical methods like FEM can also be employed for complex magnet shapes and configurations.