How do you calculate the charging and discharging times of an RC circuit?

To calculate charging and discharging times of an RC circuit, determine the time constant (τ = RC) and use exponential charging and discharging equations.

Calculating Charging and Discharging Times of an RC Circuit

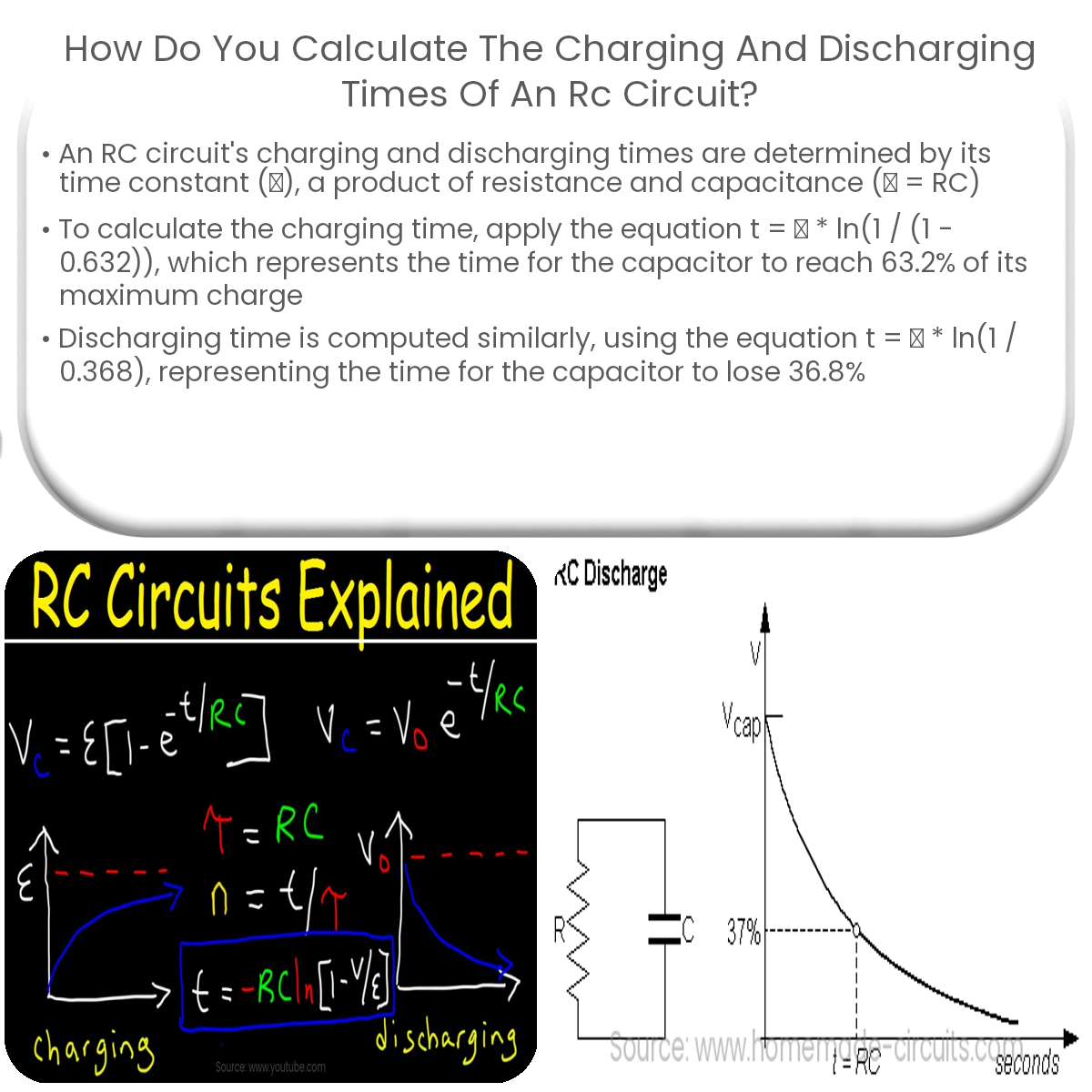
An RC circuit consists of a resistor (R) and a capacitor (C) connected in series. When a voltage is applied to the circuit, the capacitor charges and discharges over time. The charging and discharging rates are determined by the time constant (τ), which is the product of resistance and capacitance (τ = RC).

Charging Time

To calculate the charging time of an RC circuit, we first need to determine the time constant (τ). The charging process can be described by the following equation:

V_C(t) = V₀(1 – e^-t/τ)

Where V_C(t) is the voltage across the capacitor at time t, V₀ is the initial voltage across the capacitor, e is the base of the natural logarithm, and τ is the time constant.

The charging time is usually defined as the time it takes for the capacitor to reach a certain percentage of its maximum charge. A common value used is 63.2% (1 – 1/e) of its maximum charge. Using the equation above and substituting 63.2% of V₀ for V_C(t), we can solve for t:

t = τ * ln(1 / (1 – 0.632))

This gives us the charging time for the RC circuit.

Discharging Time

For the discharging process, the voltage across the capacitor decreases exponentially over time. The discharging equation is:

V_C(t) = V₀e^-t/τ

As with charging time, the discharging time is often defined as the time it takes for the capacitor to lose a certain percentage of its initial charge. A common value is 36.8% (1/e) of its initial charge. Substituting 36.8% of V₀ for V_C(t) in the equation above, we can solve for t:

t = τ * ln(1 / 0.368)

This gives us the discharging time for the RC circuit.

In summary, to calculate the charging and discharging times of an RC circuit, we first need to determine the time constant (τ) and then use the exponential charging and discharging equations to find the corresponding times for a specific percentage of the maximum or initial charge.