How do you calculate RMS voltage and current in an AC circuit?

To calculate RMS voltage and current in an AC circuit, divide the peak voltage and peak current by the square root of 2 (√2) respectively.

Calculating RMS Voltage and Current in an AC Circuit

RMS (Root Mean Square) values play a critical role in AC circuit analysis, as they offer a means to compare AC waveforms with DC voltages and currents. Understanding how to calculate RMS voltage and current is essential for any electrical engineer, technician, or hobbyist. This article will explain the process for calculating RMS values in an AC circuit.

What is RMS?

RMS stands for Root Mean Square, and it represents the effective value of an AC waveform, such as a sine wave. The RMS value allows you to compare an AC waveform to an equivalent DC value that would produce the same amount of heat or power in a resistive load. This comparison is crucial when designing and analyzing circuits that involve both AC and DC components.

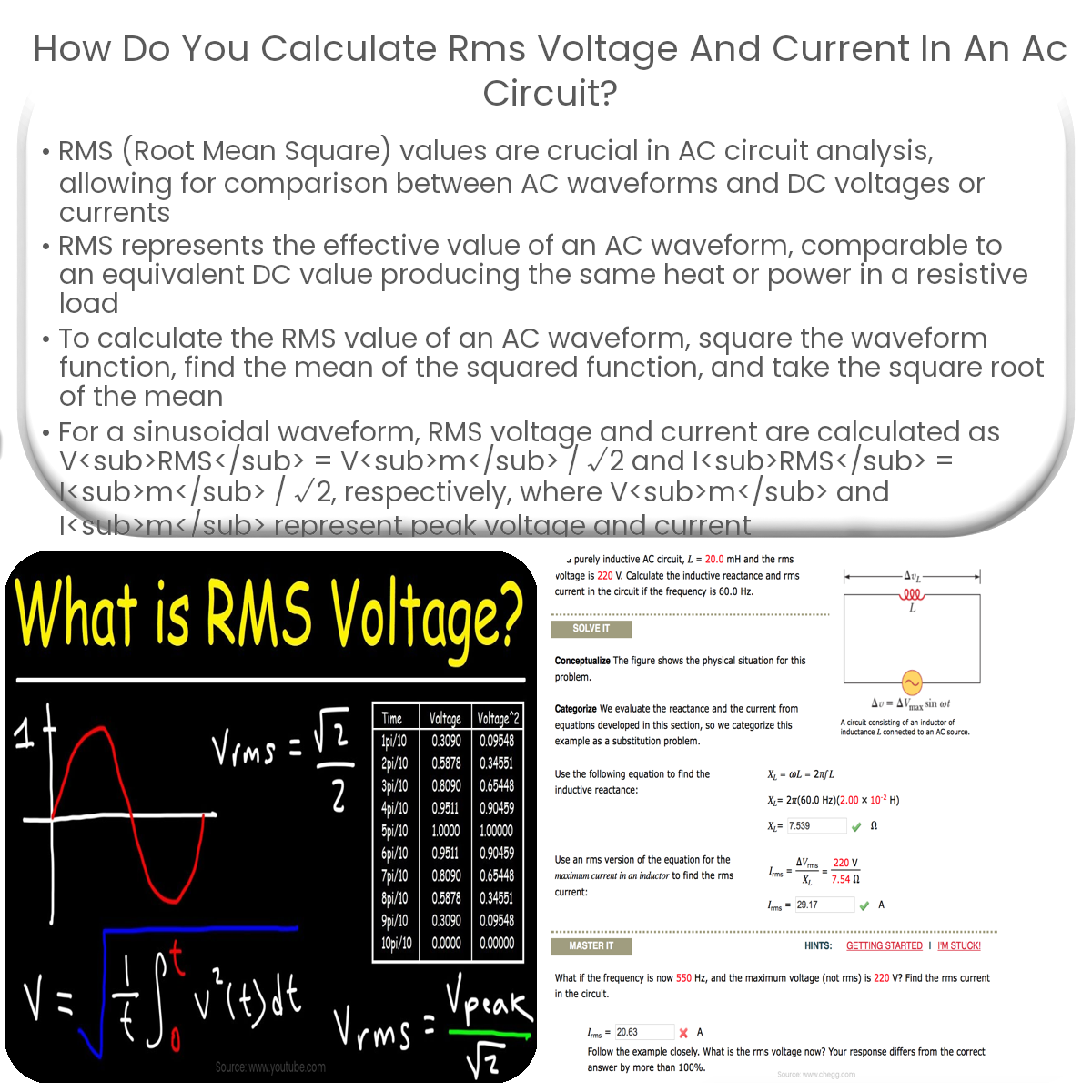
Calculating RMS Voltage and Current

To calculate the RMS value of an AC waveform, you need to follow these three steps:

1. Square the waveform function
2. Find the mean (average) of the squared function
3. Take the square root of the mean

For a sinusoidal waveform, the mathematical equation for RMS voltage (V_RMS) and RMS current (I_RMS) can be written as:

V_RMS = V_m / √2

I_RMS = I_m / √2

Where V_m and I_m represent the peak voltage and peak current, respectively.

Example

Let’s calculate the RMS voltage and current for an AC waveform with a peak voltage of 10V and a peak current of 5A.

1. Divide the peak voltage by √2 to obtain the RMS voltage: V_RMS = 10V / √2 ≈ 7.07V
2. Divide the peak current by √2 to obtain the RMS current: I_RMS = 5A / √2 ≈ 3.54A

In this example, the RMS voltage and current values are approximately 7.07V and 3.54A, respectively. These values provide a basis for comparing the AC waveform to an equivalent DC voltage and current for power and heat analysis in a resistive load.

Conclusion

Understanding how to calculate RMS voltage and current in an AC circuit is essential for accurate circuit analysis and design. By following the three-step process outlined in this article, you can easily determine the effective values of any AC waveform and make informed decisions about your electrical system’s performance.