Capacitance

Capacitance

Capacitance is defined as the ability to store an electric charge and is symbolized by the capital letter C. Any two conductors separated by an insulator (or a vacuum) form a capacitor. Commonly recognized are two closely related notions of capacitance: self-capacitance and mutual capacitance.

The capacitance between two conductors is a function only of the geometry, the opposing surface area of the conductors and the distance between them, and the permittivity of any dielectric material between them. The amount of charge stored in a capacitor is equal to its capacitance multiplied by the voltage across the capacitor:

q = CV

The proportionality constant C is called the capacitance of the capacitor. Its value depends only on the geometry of the plates and not on their charge or potential difference. The capacitance is a measure of how much charge must be put on the plates to produce a certain potential difference between them: The greater the capacitance, the more charge is required.

Capacitance (C), measured in farads, is equal to the amount of charge (q) that can be stored in a device or capacitor divided by the voltage (V) applied across the device or capacitor plates when the charge is stored.

C = q/V

Farad – Unit of Capacitance

The SI unit of capacitance is the coulomb per volt. This unit occurs so often that it is given a special name, the farad (F). 

1 farad = 1 F = 1 coulomb per volt = 1 C/V

As you will see, the farad is a very large unit. Submultiples of the farad, such as the microfarad and the picofarad, are more convenient units in practice. For example, the capacitance of flat, parallel metallic plates of area A and separation d is given by the expression below:

As can be seen, the permittivity is often represented by the relative permittivity ε_r or κ which is the ratio of the absolute permittivity ε and the vacuum permittivity ε₀.

ε_r = κ = ε/ε₀

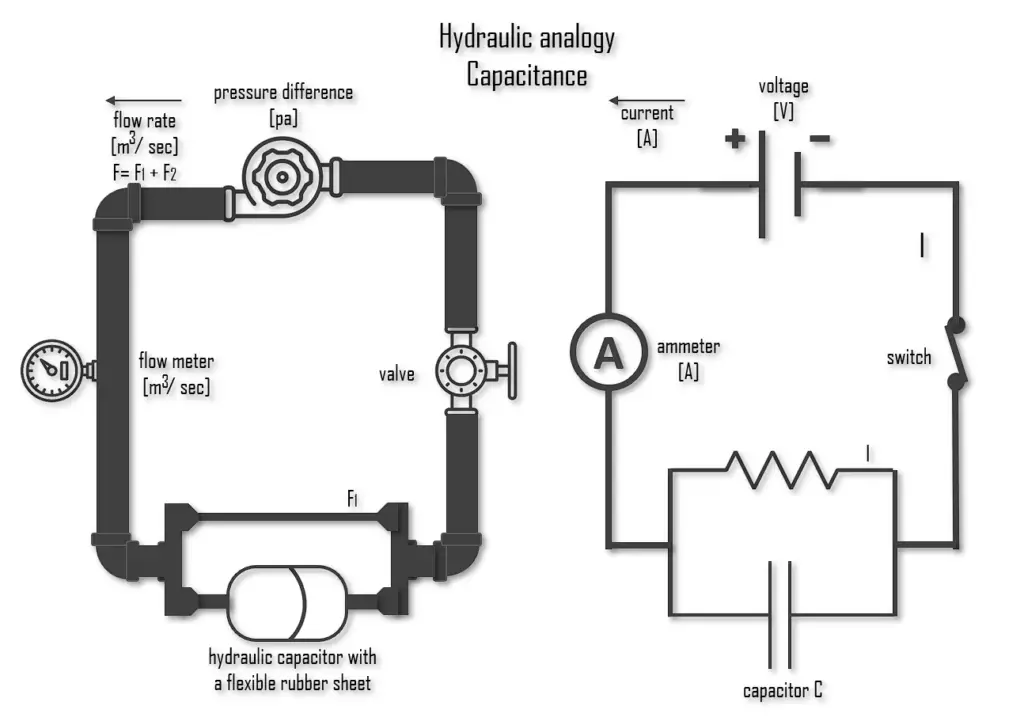
Capacitance in Hydraulic Analogy

In a hydraulic analogy, capacitors are equivalent to a tank with one connection at each end and a membrane dividing the tank in two lengthwise (a hydraulic accumulator). As the pump in the system begins pushing water, the membrane will stretch in response to the pressure from said water. The significance of the stretching is comparable to the amount of charge deposited on a capacitor. It should be fairly easy to see from this description that this membrane’s stretching represents the voltage drop in an electrical circuit, and the discharge of a capacitor is likewise comparable to the membrane returning to its original extent.

How to increase the capacitance of a capacitor

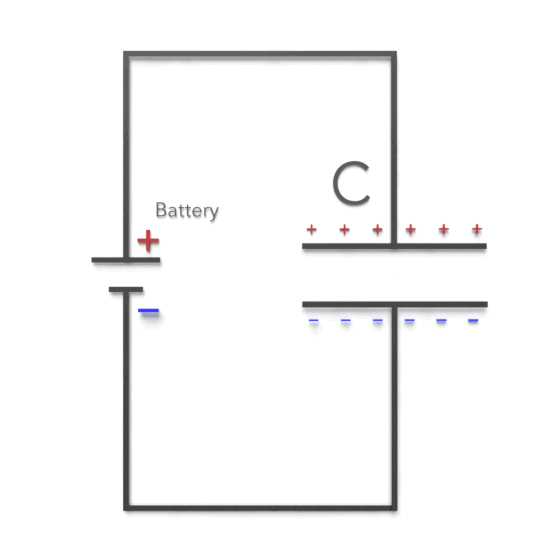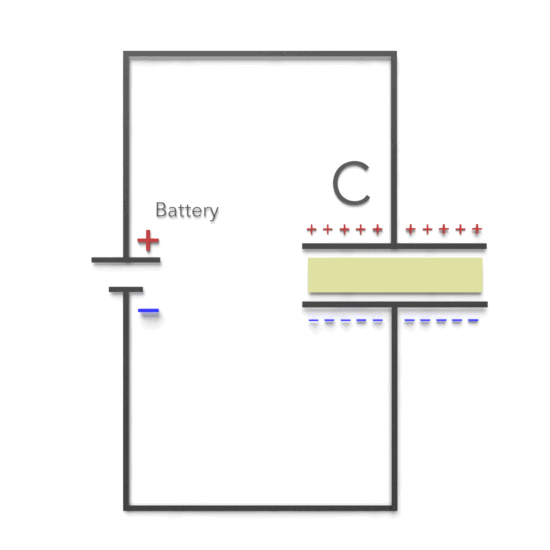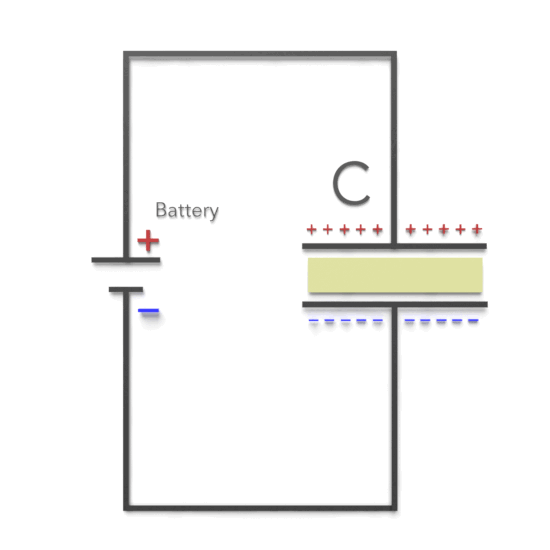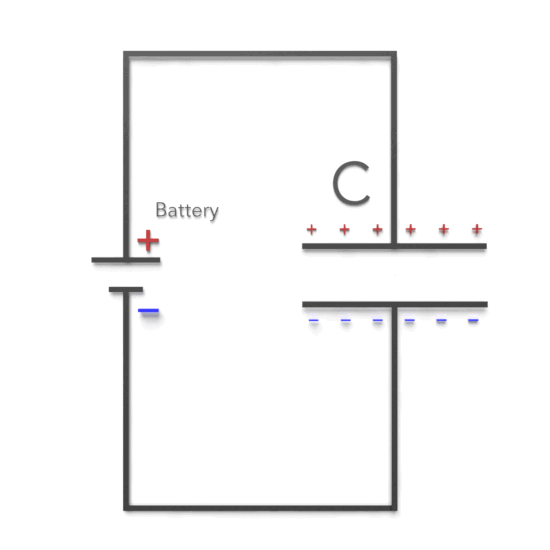
Experimentally, it was found that capacitance C increases when the space between the conductors is filled with dielectrics. The polarisation of the dielectric by the applied electric field increases the capacitor’s surface charge for the given electric field strength. The application of an electric field between the two plates induces some opposite charge on the dielectric, which opposes the applied electric field. The net result is that the electric field inside the dielectric (which fills the area between the plates) is reduced, allowing the capacitor to store more charge.

Dielectrics have many applications, but the most significant use is in capacitors. In many capacitors, there is an insulating material such as paper or plastic between the plates. Such a material, called a dielectric, can be used to maintain a physical separation of the plates.

Placing a solid dielectric between the plates of a capacitor serves three functions.

• Mechanical separation
• Electrical isolation – higher voltage possible
• Electric field reduction – higher capacitance