The capacitance of a capacitor can be calculated using the following formula:
C = Q/V
where C is the capacitance in farads (F), Q is the charge stored on the capacitor in coulombs (C), and V is the voltage across the capacitor in volts (V).
Alternatively, capacitance can be calculated using the following formula:
C = εA/d
where C is the capacitance in farads (F), ε is the permittivity of the dielectric material between the capacitor plates (in farads per meter, F/m), A is the area of the capacitor plates in square meters (m²), and d is the distance between the plates in meters (m).
Note that the above formulas assume that the capacitor is made of parallel plates with a uniform electric field between them. Real-world capacitors may have different geometries or use non-uniform dielectric materials, which can make calculating the capacitance more complicated.
In practice, the capacitance of a capacitor is typically specified by the manufacturer or measured using specialized test equipment.
Calculation of Capacitors
For example, the capacitance of flat, parallel metallic plates of area A and separation d is given by the expression below:

As can be seen, the permittivity is often represented by the relative permittivity εr or κ which is the ratio of the absolute permittivity ε and the vacuum permittivity ε0.
εr = κ = ε/ε0
Example:
The parallel plates of a ?1F capacitor are 1.0 mm apart in a vacuum. What is their area?
This problem uses the relationship among the capacitance C, plate separation d, and plate area A for a parallel-plate capacitor. We solve the equation for parallel-plate capacitor.
A = C.d/ε0 = 1.1 x 102 m2
That’s quite a large area. In reality, the capacitor can be much smaller. The trick is to have an appropriate substance between the plates rather than a vacuum, so that the plate separation d can greatly reduced.
Capacitors in series and parallel
Capacitors may be combined in series or parallel. The following figure shows three capacitors connected in series and connected to an electric source. Theoretically, the equivalent capacitance for the series connection is given by:
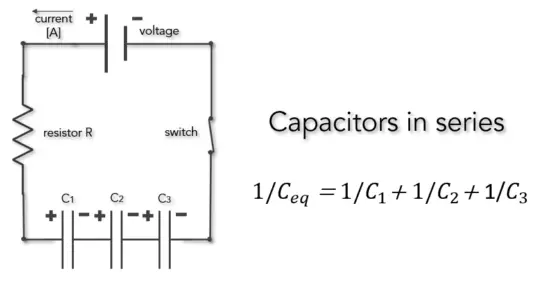
In the case of series connection of capacitors, the reciprocal of the equivalent capacitance is equal to the sum of the reciprocals of the capacitances of the capacitors.
In the case of parallel connection of capacitors, the equivalent capacity is equal to the sum of the capacities of the capacitors.
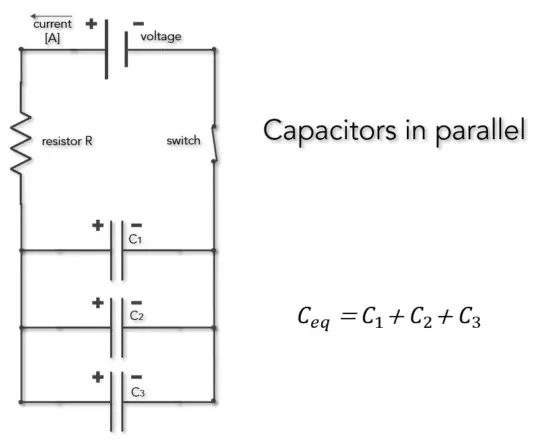
Energy stored in Capacitor
Capacitors can be used to store electrical energy. Many of the most important applications of capacitors depend on their ability to store energy. The electric potential energy stored in a charged capacitor is just equal to the amount of work required to charge it—that is, to separate opposite charges and place them on different conductors. When the capacitor is discharged, this stored energy is recovered as work done by electrical forces.
It can be derived that if, at the end of the charging process, the charge on the top plate is +Q, then the total amount of work done in this process is:
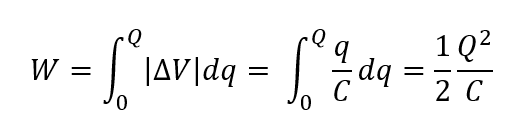
This is also equal to the total work done by the electric field on the charge when the capacitor discharges.
Typical Values
One farad of capacitance is a relatively large unit of capacitance, and it is not commonly found in most electronic circuits. A capacitor with a capacitance of one farad can store one coulomb (C) of charge per volt of potential difference between its plates. Submultiples of the farad, such as the microfarad and the picofarad, are more convenient units in practice.
To give you an idea of how large one farad is, consider the following examples:
- A typical small ceramic capacitor used in electronics might have a capacitance of around 0.1 microfarads (µF), which is one ten-millionth of a farad.
- A typical electrolytic capacitor used in power supply circuits might have a capacitance of a few hundred or thousand microfarads (µF), which is still many orders of magnitude smaller than one farad.
- A supercapacitor or ultracapacitor, which is a type of high-capacity capacitor used in some energy storage applications, might have a capacitance of several farads or even tens of farads.
In summary, one farad of capacitance is a relatively large unit of capacitance, and capacitors with capacitances in the farad range are typically only used in specialized applications. Most electronic circuits use capacitors with capacitances in the microfarad or picofarad range.

